Tutorium 05 - 17.11.2023

Korrektur Exercise-04

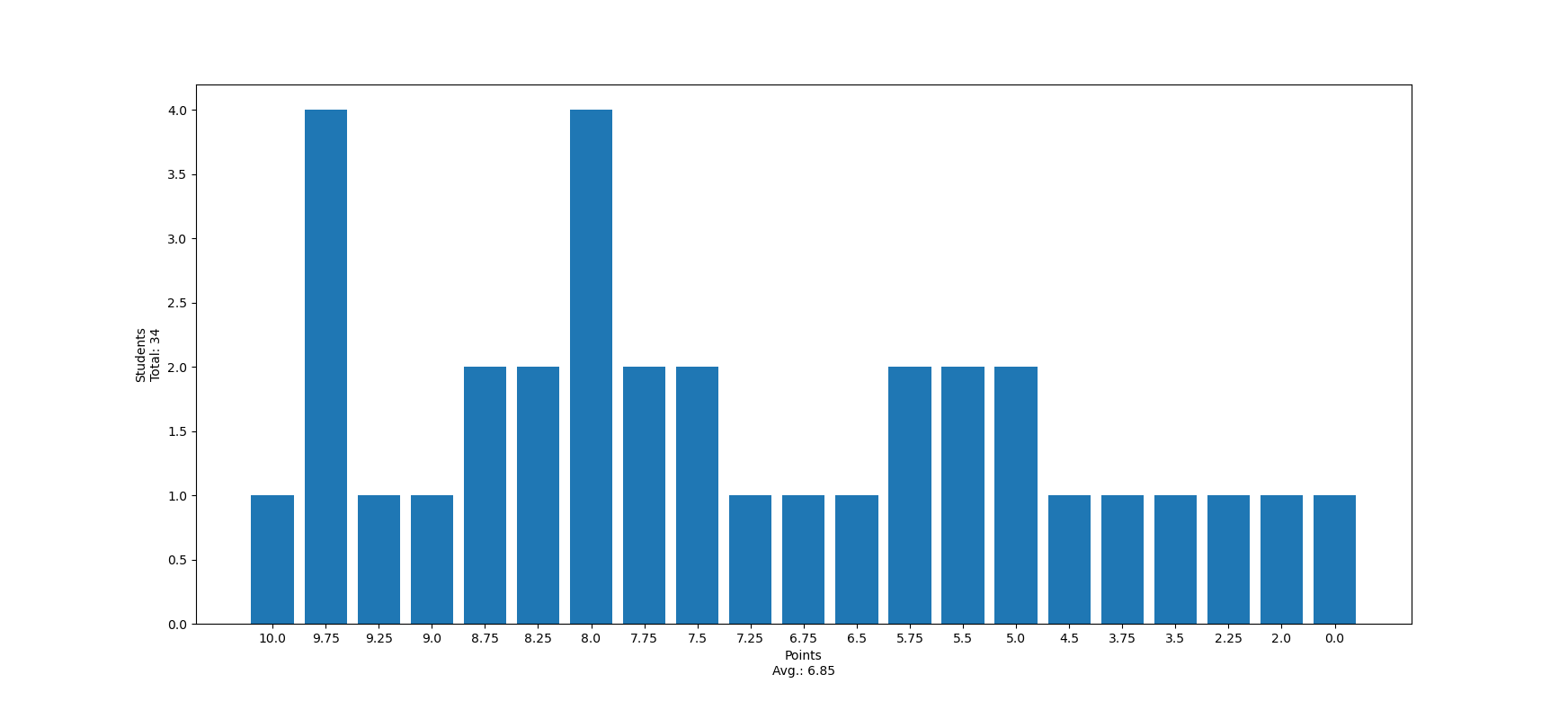
Punkteverteilung

Häufige Fehler

Type Annotations

Print-Statements, Top-Level Statements in Logik/nicht in

if __name__ == "__main__":
    assert # some test

Ich kann euch prinzipiell immer 0 Punkte geben wenn Ihr etwas verwendet, was nicht Teil der Vorlesung war
Lest die Aufgabenstellungen/Hinweise auf dem Blatt
Benennt eure Dateien/Methoden richtig

Vorrechnen

lists.py
- a) even:
- b) min:
- c) max:
euler.py
- a) fac:
- b) approx_e:
binary.py
- a) to_num:
- b) stream_to_nums:

Exercise-05

Abgabe Montag 09:00 Uhr im git
Probleme beim installieren von pygame?

Übungsaufgaben

Schreibe eine Funktion prime_factorization die eine Ganzzahl n entgegen nimmt und alle Primfaktoren berrechnet und die gegebene Zahl n in einen Paar mit den Primfaktoren als Liste zurückgibt. Denkt dabei an die richtigen Type Annotations

def prime_factorization(n):
    pass

Dataclass

Schreiben Sie eine Datenklasse Fraction (Bruch), beachten Sie dabei die Type Annotations. Ein Bruch besteht aus einem divident und einem divisor.

from dataclasses import dataclass


@dataclass
class Fraction:
   pass

Nun modellieren wir Hilfsmethoden für unsere Datenklassen, die uns später bei der Logik von Brüchen helfen

# the greatest common divisor of two numbers `a`, `b`
def gcd(a, b):
   pass

# this shortens a fraction to its most reduced representation
def shorten_fraction(fraction):
   pass

Abschließend modellieren wir nun auch noch das Verhalten von Brüchen indem wir Methoden direkt in der Datenklasse erstellen. Type Annotations!

# Multiplication of two fractions
# `Fraction(1 / 2) * Fraction(2 / 6) -> Fraction(1, 6)`
# Extra: make it possible to multiply `int` with a fraction
# `Fraction(1 / 2) * 2 -> Fraction(1 / 4)`
def __mul__(self, o):
   pass

# The division of two fraction
# `Fraction(1 / 2) / Fraction(2 / 6) -> Fraction(3, 2)`
# Extra: make it possible to divide `int` with a fraction
# `Fraction(1 / 4) / 2 -> Fraction(1 / 2)`
def __truediv__(self, o):
   pass

# The negative of a fraction
# `-Fraction(1 / 2) -> Fraction(-1 / 2)`
def __neg__(self):
   pass

# The addition of two fractions
# `Fraction(1 / 4) + Fraction(2 / 8) -> Fraction(1 / 2)`
# Extra: make it possible to add `int` with a fraction
# `Fraction(1 / 4) + 1 -> Fraction(5 / 4)`
def __add__(self, o):
   pass

# The subtraction of two fractions
# `Fraction(1 / 2) - Fraction(1 / 4) -> Fraction(1 / 4)`
# Extra: make it possible to subtract `int` with a fraction
# `Fraction(5 / 2) - 1 -> Fraction(3 / 2)`
def __sub__(self, o):
   pass

# The `equal`-function is == and should only care about reduced fractions
# `Fraction(1 / 2) == Fraction(2 / 4)` is True
def __eq__(self, o):
   pass

# The `not equal`-function is != and should only care about reduced fractions exactly as equal
def __neq__(self, o):
   pass

# The str function should return this string `(divident / divisor)`
def __str__(self):
   pass

README.md